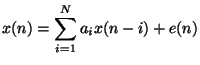
Speex is based on CELP, which stands for Code Excited Linear Prediction. This section attempts to introduce the principles behind CELP, so if you are already familiar with CELP, you can safely skip to section 3. The CELP technique is based on three ideas:
The linear prediction model represents each speech sample as linear combination of past samples, plus an error signal called the excitation (or residual).
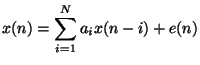
In the z-domain, this can be expressed as
where ![]() is defined as
is defined as
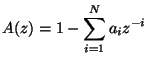
We usually refer to ![]() as the analysis filter and
as the analysis filter and ![]() as
the synthesis filter.
as
the synthesis filter.
The ![]() filter is computed using the Levinson-Durbin algorithm,
which starts from the auto-correlation
filter is computed using the Levinson-Durbin algorithm,
which starts from the auto-correlation ![]() of the signal
of the signal ![]() .
.
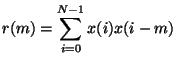
For an order ![]() filter, we have:
filter, we have:
![$\displaystyle \mathbf{R}=\left[\begin{array}{cccc}
r(0) & r(1) & \cdots & r(N-1...
... \vdots & \ddots & \vdots \\
r(N-1) & r(N-2) & \cdots & r(0)\end{array}\right]$](img10.png)
![$\displaystyle \mathbf{r}=\left[\begin{array}{c}
r(1)\\
r(2)\\
\vdots \\
R(N)\end{array}\right]$](img11.png)
The filter coefficients ![]() are found by solving the system
are found by solving the system
![]() .
What the Levinson-Durbin algorithm does here is making the solution
to the problem
.
What the Levinson-Durbin algorithm does here is making the solution
to the problem
![]() instead of
instead of
![]() by exploiting the fact that matrix
by exploiting the fact that matrix
![]() is toeplitz hermitian.
Also, it can be proved that all the roots of
is toeplitz hermitian.
Also, it can be proved that all the roots of ![]() are withing the
unit circle, which means that
are withing the
unit circle, which means that ![]() is always stable. This is
in theory; in practice because of finite precision, there are two
commonly used techniques to make sure we have a stable filter. First,
we multiply
is always stable. This is
in theory; in practice because of finite precision, there are two
commonly used techniques to make sure we have a stable filter. First,
we multiply ![]() by a number slightly above one (such as 1.0001),
which is equivalent to adding noise to the signal. Also, we can apply
a window the the auto-correlation, which is equivalent to filtering
in the frequency domain, reducing sharp resonances.
by a number slightly above one (such as 1.0001),
which is equivalent to adding noise to the signal. Also, we can apply
a window the the auto-correlation, which is equivalent to filtering
in the frequency domain, reducing sharp resonances.
During voiced segments, the speech signal is very periodic, so it
is possible to take advantage of that by expressing the excitation
signal ![]() as
as
where ![]() is the pitch period,
is the pitch period, ![]() is the pitch gain and
is the pitch gain and ![]() is taken from the innovation codebook. In the z-domain,
the excitation can be expressed as:
is taken from the innovation codebook. In the z-domain,
the excitation can be expressed as:
This is where most of the bits in a CELP codec are allocated. It represents the information that couldn't be obtained either from linear prediction or pitch prediction.
Most (if not all) modern audio codecs attempt to shape the noise so that it is the hardest to detect with the ear. That means that more noise can be tolerated in parts of the spectrum that are louder and vice versa. That's why the error is minimized for the perceptually weighted signal
with control parameters
![]() . If the noise is
white in the perceptually weighted domain, then in the signal domain
its spectral shape will be of the form
. If the noise is
white in the perceptually weighted domain, then in the signal domain
its spectral shape will be of the form
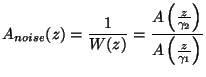
If a filter ![]() has (complex) poles at
has (complex) poles at ![]() in the
in the ![]() -plane,
the filter
-plane,
the filter
![]() filter will have its poles at
filter will have its poles at
![]() ,
making it a flatter version of
,
making it a flatter version of ![]() .
.